nsasole.blogg.se - How to find a weighted standard deviation

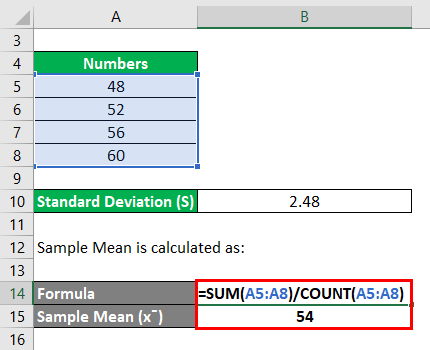
STDEV – STDEV.S was introduced in Excel 2010.Text and FALSE are taken as 0 and TRUE is taken as 1. STDEVA – Use this when you want to include text and logical values in the calculation (along with numbers).STDEV.S – Use this when your data is numeric.Now let’s understand these three formulas: this narrows down the number of formulas to three (STDEV.S, STDEVA, and STDEV function) You can read a great explanation of it here (read the first response).

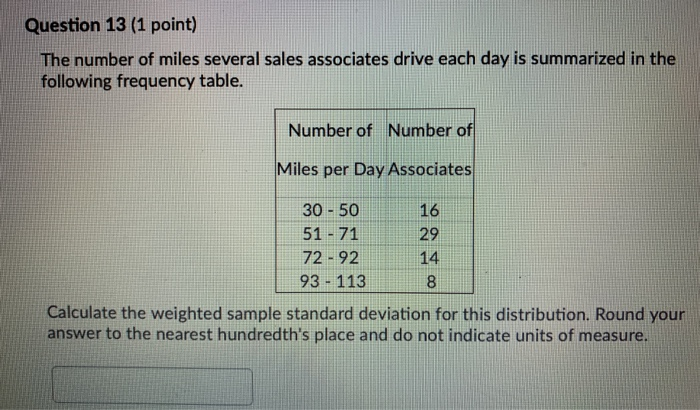
You can use the sample data to calculate the standard deviation and infer for the entire population. In such a case, you pick a sample from the population.

On the other hand, you use term ‘sample’ when using a population is not possible (or it’s unrealistic to do so). In almost all of the cases, you will use standard deviation for a sample.Īgain in layman terms, you use the term ‘population’ when you want to consider all the datasets in the entire population.

Calculating the standard deviation for an entire population: The formulas in this category are STDEV.P, STDEVPA, and STDEVP.

Calculating the sample standard deviation: The formulas in this category are STDEV.S, STDEVA, and STDEV.

These six formulas can be divided into two groups: There are six standard deviation formulas in Excel (eight if you consider database functions as well). While it’s easy to calculate the standard deviation, you need to know which formula to use in Excel. This can also be a case when there are many outliers in the data set.

A higher value indicates that there is widespread variation in the data points.

A lower value indicates that the data points tend to be closer to the average (mean) value.

Now let’s interpret the standard deviation value: It means that most of the people’s weight is within 4 kg of the average weight (which would be 56-64 kg). In this data set, the average weight is 60 kg, and the standard deviation is 4 kg.

Example – Calculating the Standard Deviation for Weight DataĪ standard deviation value would tell you how much the data set deviates from the mean of the data set.įor example, suppose you have a group of 50 people, and you are recording their weight (in kgs).

Calculating Standard Deviation in Excel.

As discussed in the next post we are actually interested in how randomly selected portfolio ’s out- or underperformance deviates from the benchmark. This is a measure of the amount by which a randomly selected stock’s out- or underperformance deviates from the benchmark, on average.

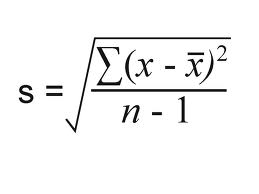
The market cap-weighted benchmark return is calculated asīenchmark return \(= \sum _ \). Th e stock weights and benchmarks returns for a measurement period are given in the graphs below: Stock C and D have market caps of 10% and 5% respectively of the total market. Stock A and Stock B have market caps equal to 45% and 35% respectively of the market’s total capitalisation. We consider a simplified stock market which consists of two large-capitalisations (cap) and two small-cap stocks. The analysis is also applicable when we compare managers against their peers. However, as preparation, we first consider market dispersion from a stock perspective.Īs before, performance is measured against the unbiased market-capitalisation (market-cap) weighted benchmark. If we want to examine how market dispersion affects manager outperformance we have to measure the dispersion of active portfolio returns instead. This measure describes the dispersion in individual stock returns. Here we explain the methodology for calculating an asset-weighted standard deviation of share returns, often also referred to as the cross-sectional standard deviation. Opportunities for successful security selection abounds when market dispersion is high, as discussed before. Market dispersion refers to the variation in returns of the market’s underlying securities.